Modeling of light scattering on a single platelet and their aggregates
Свидельская Галина Сергеевна 1,2,3* Быков Георгий Александрович 1
* Correspondence: galina.svidelskaya@gmail.com; Tel.:8-906-702-91-84
Galina S. Svidelskaya 1,2 Georgii A. Bykov 1
1.Центр теоретических проблем физико-химической фармакологии РАН Россия, 109029, г. Москва, ул. Средняя Калитниковская, д. 30
2.ФГБУ «НМИЦ ДГОИ им. Дмитрия Рогачева» Минздрава России Россия, 117997, г. Москва, ГСП-7, ул. Саморы Машела, д. 1
3.Московский государственный университет имени М.В. Ломоносова, физический факультет, кафедра медицинской физики, Россия, 119991, Москва, Ленинские горы, д. 1, стр. 2
1.Center for Theoretical Problems of Physicochemical Pharmacology Russian Academy of Sciences Moscow, 109029, Russia
2.National Medical Research Centre of Pediatric Hematology, Oncology and Immunology named after Dmitry Rogachev Moscow, 117198, Russia
3.Faculty of Physics, Lomonosov Moscow State University, 1/2 Leninskie Gory, Moscow, 119991, Russia.
EDN: BEIDSE
Аннотация
Агрегация тромбоцитов – важнейший этап формирования тромбоцитарной пробки для закупоривания места повреждения сосуда. Одним из методов оценки агрегации тромбоцитов является метод малоуглового светорассеяния. При математическом моделировании рассеяния электромагнитного излучения на тромбоците преимущественно рассматривается задача рассеяния света на тромбоците в состоянии покоя. Целью данной работы является разработка математической модели и анализ рассеяния лазерного излучения на тромбоците в состоянии покоя, а также при активации и агрегации тромбоцитов. Параметры модели подбирались автоматически по ранее опубликованным экспериментальным данным. В результате исследования получены индикатрисы рассеяния как на тромбоцитах в состоянии покоя, так и на активированных тромбоцитах, а также на их агрегатах. Обнаружено, что в условиях рассеяния света в буфере, содержащем тромбоциты (вне зависимости от статуса их активации) или их агрегаты, рассеяние преимущественно происходит вперед, что согласуется с литературными данными.
Ключевые слова: Моделирование; Светорассеяние; Лазерное излучение; Тромбоцит; Агрегация тромбоцитов
Annotation
Platelet aggregation is the most important stage in the formation of a platelet clot at the site of damage in the vessel. One of the methods for assessing platelet aggregation is the small-angle light scattering method. In mathematical modeling of electromagnetic radiation scattering on a platelet, the problem to consider is the light scattering on a platelet at rest. The purpose of this work is to develop a mathematical model and analyze the scattering of laser radiation on a platelet at rest, as well as during platelet activation and aggregation. The model parameters were selected automatically based on previously published experimental data. As a result of the study, scattering indicatrices were obtained on both platelets at rest and activated platelets, as well as on their aggregates. It was found that under conditions of light scattering in a buffer containing platelets (regardless of their activation status) or their aggregates, scattering mainly occurs forward, which is consistent with the literature data.
Key words: Modeling; Light scattering; Laser radiation; Platelet; Platelet aggregation
Введение
Тромбоциты – самые мелкие безъядерные форменные элементы крови [4], имеющие форму дисков диаметром 2-4 мкм и толщиной 0.5 мкм [1]. Повреждение сосуда и нарушение его эндотелиальной выстилки сопровождается появлением в этом участке сосудистого русла биологически активных соединений, способных активировать тромбоциты. Эти соединения называют агонистами или индукторами, и их действие направлено на стимуляцию протромбогенных реакций тромбоцитов [3]. Активация тромбоцитов в результате действия растворимых агонистов или адгезии к активному субстрату сопровождается быстрым изменением их формы – превращением дисков в частицы сферической формы, образованием выростов и псевдоподий, распластыванием при прикреплении к поверхности [6].
В 1998 г. для исследования активации и агрегации тромбоцитов был предложен новый метод оценки динамического светорассеяния [2], реализованный на приборе ЛАСКА-ТМ. Этот метод, основанный на явлении лазерной малоугловой дифракции света, предоставляет информацию об агрегации и изменении формы тромбоцитов.
Моделирование светорассеяния для валидации данных анализатора ЛАСКА-ТМ впервые было реализовано разработчиками оборудования. Миндукшев И.В. и соавторы продемонстрировали оригинальные кривые зависимости интенсивности света от угла рассеяния (индикатрисы) при активации тромбоцитов слабым агонистом [7]. При агрегации интенсивность светорассеяния увеличивается в диапазоне 1°–5° и уменьшается в диапазоне 8°–12°. Эти результаты находились в согласии с результатами, полученными при моделировании процесса. Помимо этого, этим же коллективом представлена зависимость (полученная экспериментально) интенсивности светорассеяния и светопропускания от концентрации тромбоцитов человека. В диапазоне концентрации тромбоцитов от 0 до 10 тысяч тромбоцитов/мкл интенсивность светорассеяния на 1° увеличивается, в то время как светопропускание убывает. В статье [8] приведены данные по количественному распределению АДФ-индуцированных агрегатов тромбоцитов по размерам в процессе агрегации. Авторы статьи показали, что АДФ в низких (100 нМ) концентрациях индуцировал образование небольших агрегатов, содержащих в основном 2–5 клеток. Увеличение концентрации АДФ вызывало постепенное увеличение количества крупных агрегатов.
Однако данные по индикатрисам рассеяния тромбоцитами лазерного излучения на разных этапах их активации пока скудны. Остается неясным, есть ли отличия в индикатрисах рассеяния света неактивированным и активированным тромбоцитом, а также влияет ли ориентация тромбоцита по отношению к падающему лучу на диаграммы направленности.
Целью текущей работы стало моделирование рассеяния лазерного излучения на тромбоцитах и их агрегатах для валидации данных, получаемых с помощью метода малоуглового светорассеяния. Для достижения данной цели были поставлены следующие задачи: расчёт индикатрис рассеяния на неактивированном и активированном тромбоците, а также их агрегатах; моделирование индикатрис рассеяния в образцах содержащих различную концентрацию тромбоцитов; моделирование рассеяния поляризованного и неполяризованного света на тромбоците.
Материалы и Методы
Анализ данных полученных с помощью лазерного анализатора ЛАСКА-ТМ проводился с помощью программного обеспечения ЛАСКА-32. Для расчетов использовалось оригинальное программное обеспечение LaSca_32 (ООО «БиоМедСистемы», Санкт-Петербург, Россия). Численное решение волнового уравнение для электрического поля проводилось с помощью среды Comsol Multiphysics v6.2. Для расчёта светорассеяния согласно теории Ми использовали программу MiePlot v4.6.21 [Philip Laven MiePlot. Доступно онлайн: http://www.philiplaven.com/mieplot.htm]
Результаты
Первой задачей данной работы являлось моделирование светорассеяния на одиночном тромбоците. Для решения этой задачи были использованы следующие допущения: 1) изначально тромбоцит имеет форму эллипсоида с полуосями 1 мкм, 3 мкм, 3 мкм. Тромбоцит является однородной средой относительно показателя преломления.
•При активации тромбоцит принимает форму шара. Из предположения, что объём клетки при этом остаётся постоянным, следует, что радиус этого шара составит 2.08 мкм.
•После ошаривания тромбоцита из него вырастают филоподии, таким образом, что тромбоцит принимает форму шара с восьмью выростами. Допускается, что форма выростов эллипсоидальная. В предположении, что при активации объем тромбоцита такой же как и в состоянии покоя, радиус тромбоцита в активированном состоянии равен 1.67 мкм. Длина большой полуоси эллипсоида составляет 1.8 радиусов шара, две малые полуоси эллипсоида составляют треть от радиуса шара.
• Затем тромбоциты слипаются и образуют агрегат из 6 клеточных фрагментов.
На рисунке 1 представлены трехмерные модели тромбоцитов, использованные для получения диаграмм направленности. Чтобы изложенную выше задачу можно было решить с помощью ограниченных вычислительных мощностей, от соответствующих трёхмерных фигур отрезалась четверть, на неё накладывались условия симметрии, и уже в таком виде решалась задача рассеяния.
При моделировании использованы следующие параметры:
•Длина волны излучения равна 670 нм.
•Показатель преломления тромбоцита равен 1.38 [9]
•Показатель преломления раствора (буфера), в котором он находится такой же, как и у воды и составляет 1.33.
C помощью среды Comsol Multiphysics v6.2 решается численно волновое уравнение для электрического поля (формула 1): где Е – электрическое поле, В/м, n – показатель преломления, k0 = w/c0 – волновое число раствора, w – угловая частота падающего излучения, c0 – скорость света в вакууме.
Решением данного уравнения являются диаграммы направленности излучения в дальнем поле (электрическое поле) представленные на рисунке 2. На рис. 2 показано, что вне зависимости от ориентации тромбоцита по отношению к направлению лазерного излучения, а также вне зависимости от статуса активации/агрегации тромбоцитов, максимальная интенсивность света на малых углах приходится на 0°. В интервале от 0° до 7° интенсивность светорассеяния нелинейно уменьшается. Для одиночных тромбоцитов максимум второго порядка приходится на 10.5° и 11.5° соответственно для излучения, направленного параллельно короткой и длинной оси тромбоцита.
Для неактивированного тромбоцита максимум проходящего света через частицу приходится на 0° вне зависимости от ориентации клетки по отношению к направлению падающего света (параллельно длинной оси тромбоцита или короткой). На рисунке 3 представлены диаграммы рассеяния в полярных координатах для данного случая. Превалирует рассеяние вперед. Под углами от 90° до 180° свет не рассеивается.
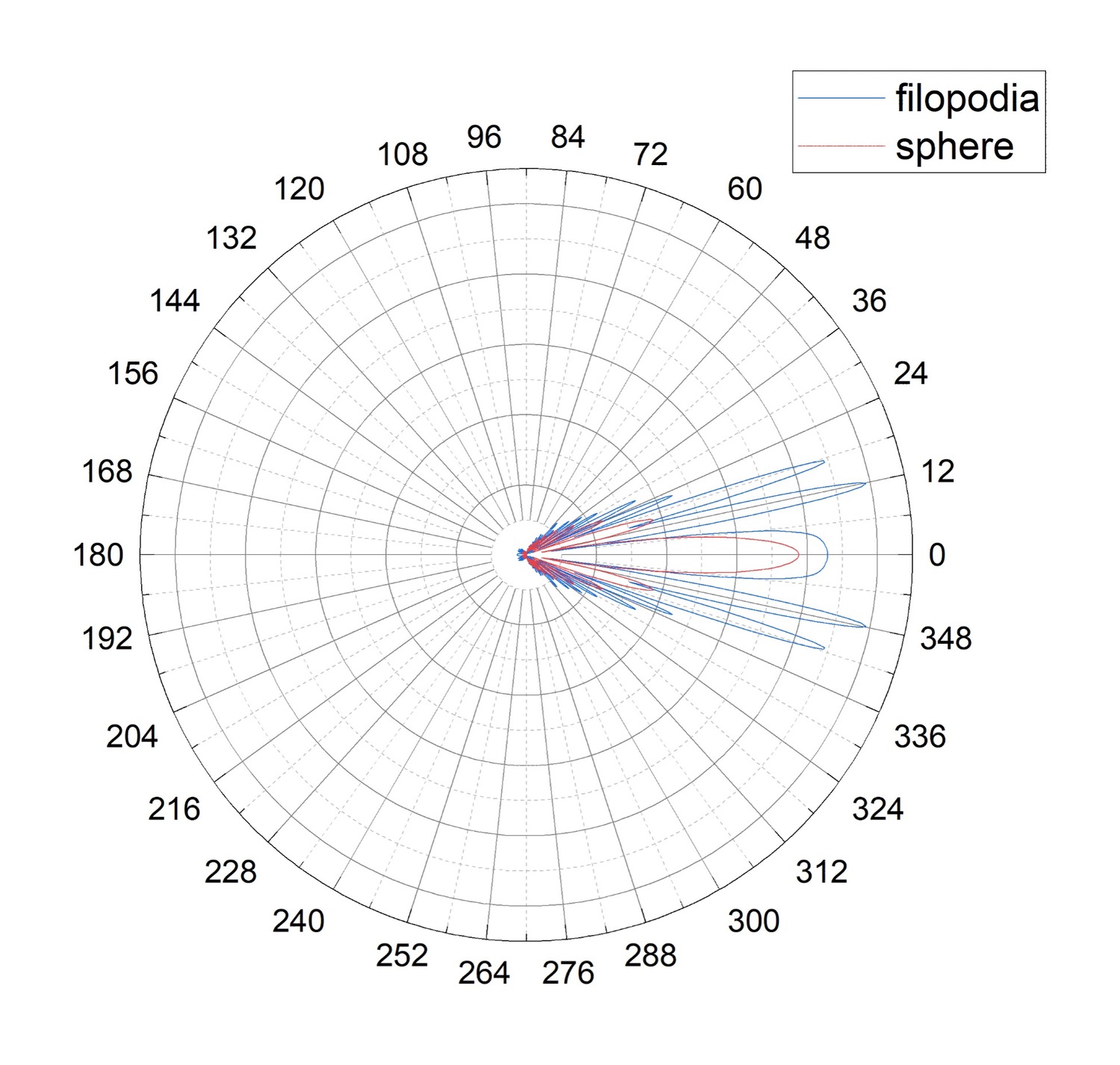
На рис. 4 представлены диаграммы рассеяния для тромбоцита выпустившего филоподии и ошаренного активированного тромбоцита. В случае активированного тромбоцита в форме сферы превалирует рассеяние перед, рассеяние назад отсутствует или пренебрежимо мало по сравнению с боковым. Максимум светорассеяния приходится на 0°. В случае тромбоцита выпустившего филоподии максимальный уровень светорассеяния приходится на 12°, а на 0° приходится локальный максимум.
На рисунке 5 представлена диаграмма направленности для агрегата из шести тромбоцитов. Максимальный сигнал светорассеяния приходится на 0°, в интервале от 0 до 6° уровень светорассеяния убывает, а в диапазоне от 6 до 12° функция является возрастающей. Как и в случае с диаграммой направленности для активированного тромбоцита для агрегата превалирует рассеяние вперед и боковое рассеяние, сигнал светорассеяния в диапазоне от 90 до 180° пренебрежимо мал по сравнению с сигналом на 0°.
Расчет индикатрис рассеяния на сферическом объекте размера порядка 2 мкмЗависимость интенсивности рассеяния света от угла, рассчитанная по теории Ми (или приближению Фраунгофера), представлена угловой диаграммой (рис. 6). Для расчета угловой диаграммы использовалась программа MiePlot v4.6.21 (www.philiplaven.com), которая позволяет рассчитывать полимодальные функции распределения частиц по размерам.
На рис. 6 видно, что максимальная интенсивность светорассеяния приходится на 0°, ближайший локальный максимум – на 12°. Характер кривых для перпендикулярно и параллельно поляризованного света сходный: интенсивность света не является монотонной зависимостью от угла рассеяния, но в целом, является убывающей от 0° до 180°. Превалирует рассеяние вперед.
На рис. 7 приведен график зависимости интенсивности светорассеяния для гексамера из тромбоцитов (агрегат из 6 форменных элементов). Радиус сферы, которая будет покрывать 6 таких тромбоцитов будет равен 3.12 мкм. На рис. 7 видно, что максимальная интенсивность светорассеяния приходится на 0°, ближайший локальный максимум приходится на 8°. Характер кривых для перпендикулярно и параллельно поляризованного света сходный: функция интенсивности рассеяния от угла не является монотонной, но имеет убывающий тренд. Превалирует рассеяние вперед. На интервале от 0° до 100° имеет 20 максимумов для перпендикулярно поляризованного света.
Зависимость интенсивности светорассеяния от количества частицДля выявления зависимости интенсивности светорассеяния от количества частиц на оптическом пути был проведен численный расчет индикатрис рассеяния. Численно интенсивность равна усредненной за период колебаний волны мощности излучения, проходящей через единичную площадку, расположенную перпендикулярно направлению распространения энергии (формула 2).
При мощности лазера P равной 5мВт и диаметре пучка на выходе d1 равным 1 мм, интенсивность падающего света I0 равна (формула 3), при условии, что площадь пучка S0 равна (π*(1мм)2)/4 =0.79мм2.
Пусть радиус активированного тромбоцита r2 равен 1.5 мкм, тогда поперечная площадь тромбоцита S рассчитывается по формуле π*r22 и составит 7.07 мкм2. Положим, что N – концентрация тромбоцитов в единице освещенного объема.
Концентрация тромбоцитов в кювете равна 10 000 тромбоцитов/ мкл или 10 000 тромбоцитов в одном кубическом миллиметре. Освещается цилиндр диаметром 1 мм, длиной 10 мм (длина оптического пути). Объём такого цилиндра 0.79 мм3. В данном объёме будет находиться 78 540 тромбоцитов, общей площадью 0.56 мм2 (рис. 8). Если I0 – интенсивность падающего света, тогда интенсивность прошедшего сквозь кювету света Ip будет изменятся по закону (формула 4), где первое слагаемое отражает часть нерассеянного света (β=0), а второе слагаемое соответствует рассеивающему члену.
Интенсивность рассеянного света от каждой частицы I(β) равна (формула 5), где k — волновое число равное 2π/λ (λ — длина волны света), a — расстояние от рассеивающего объекта до детектора, x представляет собой безразмерный параметр размера равный π*d/ λ, (d — диаметр частицы), J1 – сферическая функция Бесселя первого порядка. Формула заимствована из [7].
Рассмотрим ряд случаев для расчёта интенсивности светорассеяния при направлении лазерного излучения на измерительную кювету:
1.Буфер в кварцевой кюветеЕсли рассеивающих объектов нет, т.е. кювета не содержит тромбоцитов, тогда интенсивность падающего света равна интенсивности прошедшего насквозь пучка (формула 6).
2.Взвесь активированных тромбоцитов в буфереВведем переменную ɤ равную x*sinβ, тогда сферическая функция Бесселя первого порядка определяется выражением (формула 7).
Если β=0, то ɤ=0 и для J1(ɤ)/ɤ возникает неопределенность типа 0/0. По этой причине проведение расчета индикатрисы рассеяния по формуле (1) затруднено с помощью редактора Visual Code. В виду этого интенсивность светорассеяния рассчитывалась для углов от 0.25° до 12.5° с шагом в 0.25°. График зависимости интенсивности светорассеяния от угла рассеяния в интервале от 0° до 12° представлен на рисунке 9 (черная кривая). При β равном 0.25° интенсивность света составляет около 32 кВт/м2. Если β=1°, то исходя из расчетов Ip =2 кВт/м2. Значит, интенсивность рассеяния на 0° больше чем на 1°. Также на основании этого графика можно предположить, что при устремлении угла рассеяния к 0° интенсивность светорассеяния устремляется к максимальному значению. С увеличением угла от 1° до 12° интенсивность светорассеяния падает, при этом в интервале от 2° до 12° зависимость слабая.
3. Активированные тромбоциты в агрегате
Если агрегат представляет собой гексамер (агрегат из шести сфер диаметром 3мкм), то радиус такой сферы будет равен 4.5 мкм, диаметр 9 мкм. Количество таких агрегатов в выделенном объеме составит 13 090 штук.
Выполнив подстановку соответствующих параметров в формулу (1) получено, что интенсивность нерассеянного света Ip (β=0.25) = 8400 Вт/м2
Таким образом, при увеличении размеров рассеивателей в несколько раз интенсивность светорассеяния под углом 0.25° снижается в 4 раза.
Исходя из расчетов, Ip(β=1°) равна 3385.94 Вт/м2. Интенсивность светорассеяния на 1° для рассеяния агрегатами из сфер меньше чем на 0°. При увеличении угла в интервале от 1° до 12° интенсивность светорассеяния агрегатами падает (рис. 9, красная кривая), в этом интервале зависимость слабая.
Помимо прочего была проанализирована зависимость интенсивности светорассеяния на одном градусе от концентрации частиц в растворе. В роли частиц выступили одиночные тромбоциты и их агрегаты, гексамеры. Графики зависимости представлены на рисунке 10. Было обнаружено, что интенсивность светорассеяния на 1° линейно убывает с увеличением частиц в кювете вне зависимости от размера частиц (мономеры тромбоцитов или гексамеры).
Таким образом, в ходе моделирования процесса рассеяния лазерного излучения на частице размера порядка микрометра было получено, что рассеяние преимущественно происходит вперед и вбок и имеет центральный максимум на 0°. Зависимости для кривых полученных на 1° и 12° могут предоставлять дополнительную информацию об изменении формы одной частицы (с эллипсоидальной на сфероидальную), а также и об изменении размера частиц (например, при их агрегации).
Обсуждение результатов
Моделирование светорассеяния на тромбоцитах важно по нескольким причинам, охватывающим как фундаментальные научные исследования, так и клиническую диагностику. Данная работа продолжает исследования рассеяния лазерного излучения на тромбоцитах [5], [10]. Она посвящена изучению диаграмм направленности электромагнитного излучения при рассеянии света на тромбоците или их агрегатах.
В рамках данной работы впервые разработана математическая модель, описывающая диаграммы направленности электромагнитного поля, рассеянного на неактивированной тромбоците, а также тромбоците, выпустившем филоподии. А также приведены диаграммы рассеяния поляризованного и неполяризованного света на тромбоците и/или их агрегатах. Данная модель учитывает размер тромбоцита, показатель преломления как внешней среды, так и внутренней. Полученные результаты согласуются с существующими литературными данными [7]. В ходе работы было показано, что интенсивность светорассеяния на 1° линейно убывает с увеличением концентрации частиц вне зависимости от их размера.
Тем не менее, построенная модель не свободна от ограничений. Модель не учитывает сложность формы тромбоцита, строго говоря, этот клеточный фрагмент не является эллипсоидом. Модель также не предусматривает, что показатель преломления не является постоянной величиной: у цитоплазмы, мембраны и органелл тромбоцита он разный.
В перспективе дальнейшей работы планируется учесть вышеописанные факторы, а также расширить данные на пациентов с большими (макротромбоцитопения) и маленькими (микротромбоцитопения) тромбоцитами и, таким образом, оценить вклад размера тромбоцита при рассеянии лазерного излучения. В будущем исследование планируется дополнить сопоставлением полученных результатов с экспериментальными данными.
В заключение, моделирование светорассеяния на тромбоцитах является важным инструментом для углубленного понимания биологии тромбоцитов, разработки новых диагностических методов и оптимизации существующих технологий в гематологии.
Вклад авторов
Б.Г.А. выполнял моделирование процессов, анализировал данные, писал и редактировал текст статьи; С.Г.С. руководила проектом, планировала исследования, анализировала данные, писала и редактировала текст статьи.
Благодарности
Авторы статьи выражают глубокую признательность коллективу лаборатории молекулярных механизмов гемостаза ЦТП ФХФ РАН за конструктивную критику и поддержку работы на общеинститутских семинарах.
Финансирование
Это исследование не получало внешнего финансирования
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
1. Васильев С. А. и др. Клинико-лабораторная диагностика нарушений функций тромбоцитов // 2013.
2. Деркачев Э. Ф. и др. Способ исследования активации и агрегации тромбоцитов: Патент RU 2108579 C1 6 G01 N 33/49.—1998 // БИ № 10 (II).
3. Мазуров А. В. Физиология и патология тромбоцитов. : Литтерра, 2011.
4. Пономаренко Е. А. Исследование функциональной активности тромбоцитов при стимуляции АДФ методом проточной цитометрии : диссертация на соискание ученой степени кандидата биологических нау // 2023.
5. Lattmer P., Born G. V. R., Michal F. Application of light-scattering theory to the optical effects associated with the morphology of blood platelets // Archives of Biochemistry and Biophysics. 1977. Т. 180. № 1. С. 151–159.
6. Linden M. D. Platelet physiology. // Methods Mol Biol. 2013. Т. 992. С. 13–30.
7. Mindukshev I. и др. Low angle light scattering analysis: a novel quantitative method for functional characterization of human and murine platelet receptors. // Clin Chem Lab Med. 2012. Т. 50. № 7. С. 1253–1262.
8. Mindukshev I. и др. Platelet Hemostasis Reactions at Different Temperatures Correlate with Intracellular Calcium Concentration. // Int J Mol Sci. 2022. Т. 23. № 18.
9. Moskalensky A. E. и др. Accurate measurement of volume and shape of resting and activated blood platelets from light scattering. // J Biomed Opt. 2013. Т. 18. № 1. С. 17001.
10. Strokotov D. I. и др. Polarized light-scattering profile-advanced characterization of nonspherical particles with scanning flow cytometry. // Cytometry A. 2011. Т. 79. № 7. С. 570–579.